-
PDF
- Split View
-
Views
-
Cite
Cite
Jo Nishino, Detecting Selection Using Time-Series Data of Allele Frequencies with Multiple Independent Reference Loci, G3 Genes|Genomes|Genetics, Volume 3, Issue 12, 1 December 2013, Pages 2151–2161, https://doi.org/10.1534/g3.113.008276
Close - Share Icon Share
Abstract
Recently, in 2013 Feder et al. proposed the frequency increment test (FIT), which evaluates natural selection at a single diallelic locus by the use of time-series data of allele frequencies. This test is unbiased under conditions of constant population size and no sampling noise. Here, we expand upon the FIT by introducing a test that explicitly allows for changes in population size by using information from independent reference loci. Various demographic models suggest that our proposed test is unbiased irrespective of fluctuations in population size when sampling noise can be ignored and that it has greater power to detect selection than the FIT if sufficient reference loci are used.
In population genetics, most data are obtained from a single point in time. When genetic time-series data are available, the use of such data to detect and estimate natural selection is an attractive concept. Time-series data may have direct information about natural selection because they affect allele frequencies in time. Bollback et al. (2008) introduced a statistical framework for estimating and testing natural selection by using time-series data of allele frequencies at a single diallelic locus. These authors applied their framework to an ancient human DNA sequence (Hummel et al. 2005) and a sample from an experimental evolution study of the bacteriophage, MS2 (Bollback and Huelsenbeck 2007).
Recent advances in high-throughput sequencing technology, including pooled DNA sequencing, have facilitated the acquisition of time-series data, and Bollback et al.’s (2008) method has been extended to more complicated situations. Mathieson and McVean (2013) applied a lattice model of population subdivision that enabled joint estimation of migration rate and spatially varying selection coefficients. The allele age also is an important parameter in selection inferences because it can provide information regarding the origin of a particular phenotype associated with the allele. Malaspinas et al. (2012) developed a method to estimate the selection coefficient and the allele age simultaneously. In addition, there has been increasing numbers of studies in which researchers focus on specific settings in each evolutionary experiment (e.g., Illingworth and Mustonen 2011; Gallet et al. 2012; Illingworth et al. 2012).
Feder et al. (2013) reported recently that Bollback et al.’s (2008) standard χ2-based test for selection is biased for realistic data with few sampled time points. When the number of sampled time points is sufficiently large, the likelihood ratio statistic (LRS) follows a χ2 distribution. However, the actual number of sampled time points rarely exceeds a few dozen. Particularly, when the null hypothesis is composite and the profile likelihood is used, the estimation of nuisance parameters can substantially bias inferences of the parameters of interest (e.g., see Chapter 10 of Pawitan 2001). For the problem described in this report, the nuisance parameter is the population size.
The FIT treats the nuisance parameter, N, as an unknown parameter instead of estimating it. When Yi for any i follows the normal distribution with the same variance under the null model, the FIT is an exact and unbiased test. Feder et al. (2013) verified that actual type I error rates approach the nominal significance level for various parameter settings. These investigators also demonstrated that the power of the FIT is equal to or greater than that of the ELRT. Although the FIT does not account for the sampling process from a population explicitly, the test was shown to work well even when the sampling process exists if the sample size is not small.
The FIT is a simple and bias-controlled method to detect selection. However, it is not clear whether the FIT works well when the population size fluctuates. Theoretically, under the null model with fluctuating population size Yi does not follow the same normal distribution for all i, and therefore, tFIT (Data) does not follow the Student’s t distribution.
This study is an extension of Feder et al.’s (2013) FIT that allows for fluctuations in population size by using reference loci. First, the FIT’s actual type I error rates in a fluctuating population is investigated. Then, a new test is introduced, the frequency increment test with reference loci (FITR). Given a fluctuating population size, the FITR’s actual type I error rates are almost the same as the nominal significance level. Then, the powers of the FITR and the FIT to detect natural selection were evaluated. Finally, the simulation method used in this study was validated and the properties of the FITR in practical situations were investigated. Model descriptions are presented just below and added before introducing the FITR.
Materials and Methods
Model and simulation methods
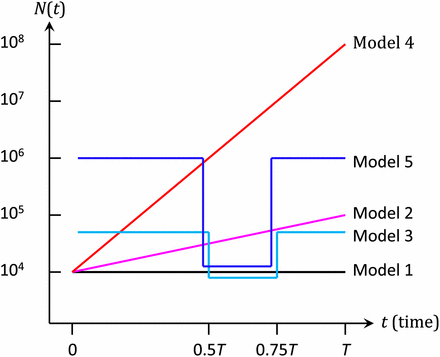
Let us consider a population evolving according to the Wright–Fisher model with fluctuating population size. The population size fluctuates as a function of generation time, t, and is denoted by N(t). To investigate the actual type I errors and the powers of Feder et al.’s (2013) FIT and the FITR introduced in this study, we conducted computer simulations under the five demographic models shown in Figure 1. The two alleles at a diallelic locus of interest are denoted by A0 and a0, respectively. At generation times , the frequencies of a0 are denoted by . Here, t0 = 0 and tL = T are the first and the last sampling times, respectively, and the number of sampled times is L + 1. The fitnesses of genotypes A0A0, A0a0, and a0a0 are assumed to be 1, , and , respectively (i.e., no dominance is assumed). The population size, N(t), is independent of the frequency of a0. As described in the next section, the FITR also uses neutral reference loci.
Demographic models used in this study. Model 1: constant-size model (N(t) = 104); Model 2: slow-growth (grows exponentially from N(0) = 104 to N(T) = 105); Model 3: moderate-bottleneck model (); Model 4: rapid-growth model (); Model 5: severe-bottleneck model ().
In the Wright–Fisher model, the allele frequency can be obtained exactly every generation as a binomial distribution. However, the generation of these data poses an extreme computational burden that is impractical for large populations (Figure 1). To avoid this burden and simulate changes in allele frequencies, we applied the pseudo-sampling method (Kimura and Takahata 1983), which is an improved version of the methods of Kimura (1980). In this method, to determine the allele frequency every generation, a uniform random number with the same mean and variance as those of the exact binomial distribution is used when the allele frequency is moderate. When the allele frequency is high or low, a Poisson random number with the same mean as that of the exact binomial random number is used. In this study, a frequency of ≤5 minor alleles in the population was used as the criteria for high or low allele frequencies. In addition, the normal distribution was used instead of the uniform distribution because the normal distribution better approximates the binomial distribution, which next-generation allele frequencies follow under the Wright–Fisher model.
Results and Discussion
Type I error rate of FIT
Table 1 summarizes the actual type I error rates for Feder et al.’s (2013) FIT. In demographic model 1 (constant-size model), as shown by Feder et al. (2013), the actual type I error rates approach the nominal level. For model 2 (slow-growth model) and model 3 (moderate-bottleneck model), the test becomes somewhat conservative. For the purposes of controlling type I error, this is a desirable property. However, in model 4 (rapid-growth model) and model 5 (severe-bottleneck model), the test tends to be too conservative, causing it to have less power to detect selection when the population size is fluctuating.
Actual type I error rates (%) of FIT
| T . | L . | Δta . | Model 1 . | Model 2 . | Model 3 . | Model 4 . | Model 5 . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 4.33 | 4.20 | 1.05 | 1.30 |
| 100 | 20 | 5 | 4.96 | 4.81 | 4.70 | 3.32 | 3.42 |
| 1000 | 200 | 5 | 4.89 | 4.90 | 4.97 | 4.87 | 4.87 |
| 10 | 5 | 2 | 4.96 | 4.23 | 3.99 | 0.48 | 0.63 |
| 100 | 5 | 20 | 4.90 | 4.03 | 4.06 | 0.44 | 0.68 |
| 1000 | 5 | 200 | 5.30 | 4.17 | 4.36 | 0.49 | 0.72 |
| T . | L . | Δta . | Model 1 . | Model 2 . | Model 3 . | Model 4 . | Model 5 . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 4.33 | 4.20 | 1.05 | 1.30 |
| 100 | 20 | 5 | 4.96 | 4.81 | 4.70 | 3.32 | 3.42 |
| 1000 | 200 | 5 | 4.89 | 4.90 | 4.97 | 4.87 | 4.87 |
| 10 | 5 | 2 | 4.96 | 4.23 | 3.99 | 0.48 | 0.63 |
| 100 | 5 | 20 | 4.90 | 4.03 | 4.06 | 0.44 | 0.68 |
| 1000 | 5 | 200 | 5.30 | 4.17 | 4.36 | 0.49 | 0.72 |
Values indicate the actual type I error rates obtained by 100,000 simulations under a nominal significance level of 5%. The initial allele frequency, x0,0, was assumed to be 0.5. FIT, frequency increment test.
.
| T . | L . | Δta . | Model 1 . | Model 2 . | Model 3 . | Model 4 . | Model 5 . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 4.33 | 4.20 | 1.05 | 1.30 |
| 100 | 20 | 5 | 4.96 | 4.81 | 4.70 | 3.32 | 3.42 |
| 1000 | 200 | 5 | 4.89 | 4.90 | 4.97 | 4.87 | 4.87 |
| 10 | 5 | 2 | 4.96 | 4.23 | 3.99 | 0.48 | 0.63 |
| 100 | 5 | 20 | 4.90 | 4.03 | 4.06 | 0.44 | 0.68 |
| 1000 | 5 | 200 | 5.30 | 4.17 | 4.36 | 0.49 | 0.72 |
| T . | L . | Δta . | Model 1 . | Model 2 . | Model 3 . | Model 4 . | Model 5 . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 4.33 | 4.20 | 1.05 | 1.30 |
| 100 | 20 | 5 | 4.96 | 4.81 | 4.70 | 3.32 | 3.42 |
| 1000 | 200 | 5 | 4.89 | 4.90 | 4.97 | 4.87 | 4.87 |
| 10 | 5 | 2 | 4.96 | 4.23 | 3.99 | 0.48 | 0.63 |
| 100 | 5 | 20 | 4.90 | 4.03 | 4.06 | 0.44 | 0.68 |
| 1000 | 5 | 200 | 5.30 | 4.17 | 4.36 | 0.49 | 0.72 |
Values indicate the actual type I error rates obtained by 100,000 simulations under a nominal significance level of 5%. The initial allele frequency, x0,0, was assumed to be 0.5. FIT, frequency increment test.
.
Frequency increment test with reference loci (FITR)
Here we propose a new test, the FITR. Consider R reference loci in addition to the focal locus. It is assumed that these loci are evolving independently and that R reference loci are evolving under neutrality. We denote by the population frequencies of one allele at the h-th reference diallelic locus at times . Recall that x0,i is the allele frequency of the focal locus at ti. Suppose that N(t) is a step function and let Ni be the population size from to such that . Note that although the following FITR discussion assumes is a step function, the same discussion can apply even the case that N(t) is a continuous function (Figure 1) because Ni can be interpreted as the variance effective size over the period from . For this reason, the FITR is unbiased irrespective of fluctuations in population size.
Type I error rate of FITR and powers of FITR and FIT
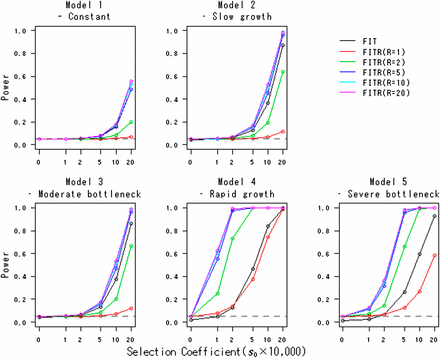
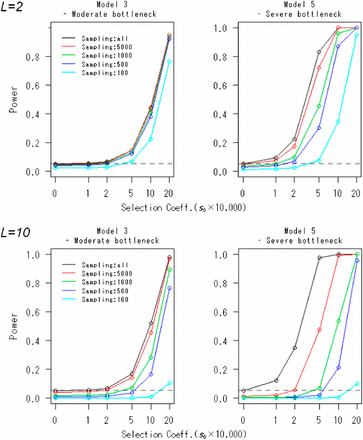
Table 2 shows the actual type I error rates of the FITR. As expected, for all demographic models, the actual type I error rates are close to the nominal level. Figure 2 shows the powers of the FITR and the FIT as a function of the strength of selection. In all demographic models, including the constant-size model, the FITR had more power than the FIT if five or more reference loci were used. For model 2 (slow-growth model) and model 3 (moderate-bottleneck model), the power of the FIT was acceptable. However, for model 4 (rapid-growth model) and model 5 (severe-bottleneck model), the power of the FIT was relatively small, and the FITR demonstrated much larger power than the FIT.
Actual type I error rates (%) of FITR
| T . | L . | Δta . | Model 1 (R = 5)b . | Model 2 (R = 2) . | Model 3 (R = 20) . | Model 4 (R = 1) . | Model 5 (R = 10) . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 5.02 | 4.95 | 5.12 | 5.00 |
| 100 | 20 | 5 | 5.09 | 4.95 | 5.06 | 5.05 | 5.00 |
| 1000 | 200 | 5 | 5.07 | 4.95 | 5.01 | 5.02 | 5.24 |
| 10 | 5 | 2 | 4.98 | 4.94 | 5.06 | 4.95 | 4.94 |
| 100 | 5 | 20 | 4.98 | 5.17 | 5.20 | 4.90 | 5.02 |
| 1000 | 5 | 200 | 4.87 | 5.02 | 5.06 | 4.89 | 5.02 |
| T . | L . | Δta . | Model 1 (R = 5)b . | Model 2 (R = 2) . | Model 3 (R = 20) . | Model 4 (R = 1) . | Model 5 (R = 10) . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 5.02 | 4.95 | 5.12 | 5.00 |
| 100 | 20 | 5 | 5.09 | 4.95 | 5.06 | 5.05 | 5.00 |
| 1000 | 200 | 5 | 5.07 | 4.95 | 5.01 | 5.02 | 5.24 |
| 10 | 5 | 2 | 4.98 | 4.94 | 5.06 | 4.95 | 4.94 |
| 100 | 5 | 20 | 4.98 | 5.17 | 5.20 | 4.90 | 5.02 |
| 1000 | 5 | 200 | 4.87 | 5.02 | 5.06 | 4.89 | 5.02 |
Values indicate the actual type I error rates obtained by 100,000 simulations under a nominal significance level of 5%. The initial frequencies for all R +1 loci, xh,0, are assumed to be 0.5. FITR, frequency increment test with reference loci.
.
The numbers of reference loci, R, are randomly assigned to each demographic model.
| T . | L . | Δta . | Model 1 (R = 5)b . | Model 2 (R = 2) . | Model 3 (R = 20) . | Model 4 (R = 1) . | Model 5 (R = 10) . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 5.02 | 4.95 | 5.12 | 5.00 |
| 100 | 20 | 5 | 5.09 | 4.95 | 5.06 | 5.05 | 5.00 |
| 1000 | 200 | 5 | 5.07 | 4.95 | 5.01 | 5.02 | 5.24 |
| 10 | 5 | 2 | 4.98 | 4.94 | 5.06 | 4.95 | 4.94 |
| 100 | 5 | 20 | 4.98 | 5.17 | 5.20 | 4.90 | 5.02 |
| 1000 | 5 | 200 | 4.87 | 5.02 | 5.06 | 4.89 | 5.02 |
| T . | L . | Δta . | Model 1 (R = 5)b . | Model 2 (R = 2) . | Model 3 (R = 20) . | Model 4 (R = 1) . | Model 5 (R = 10) . |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 5 | 4.99 | 5.02 | 4.95 | 5.12 | 5.00 |
| 100 | 20 | 5 | 5.09 | 4.95 | 5.06 | 5.05 | 5.00 |
| 1000 | 200 | 5 | 5.07 | 4.95 | 5.01 | 5.02 | 5.24 |
| 10 | 5 | 2 | 4.98 | 4.94 | 5.06 | 4.95 | 4.94 |
| 100 | 5 | 20 | 4.98 | 5.17 | 5.20 | 4.90 | 5.02 |
| 1000 | 5 | 200 | 4.87 | 5.02 | 5.06 | 4.89 | 5.02 |
Values indicate the actual type I error rates obtained by 100,000 simulations under a nominal significance level of 5%. The initial frequencies for all R +1 loci, xh,0, are assumed to be 0.5. FITR, frequency increment test with reference loci.
.
The numbers of reference loci, R, are randomly assigned to each demographic model.
Powers of the FITR and the FIT in various demographic models. Powers of the FIT (black line) and the FITR with R reference loci (colored lines) are shown as functions of the selection coefficients in the five demographic models. Each point corresponds to the power obtained by 100,000 simulations at the 5% significance level. The duration of sampling time and the number of sampled points were T = 1000 and (L + 1) = 11, respectively. The intervals between any two adjacent sampled points were the same at . The initial frequency for all R+ 1 loci, , was assumed to be 0.5.
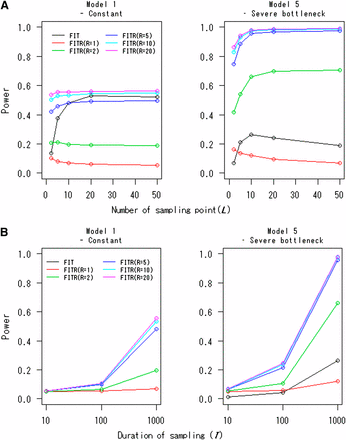
Figure 3A displays the powers of the FITR and the FIT as functions of the number of sampling points, L. In many cases, the powers approached certain asymptotic values with increasing L. In this case, the values of L for which the powers approached their asymptotes were relatively small (e.g., L = 10 or 20). The powers of the FITR for R = 1 or 2 in Model 1 decreased somewhat as the sampling points increased. This trend also was observed for the FITR with R = 1 and for the FIT in Model 5. The powers of the FITR and the FIT as functions of the duration of sampling time, T, are given in Figure 3B. For all cases, the powers increased with increasing T, as expected. For Figure 3, A and B, the FITR had more power than the FIT if 10 or more reference loci were used even in the constant-size model. This difference in power was more obvious for model 5 (severe-bottleneck model).
Powers of the FITR and the FIT as functions of (A) the number of sampling points and (B) the duration of sampling. Powers of the FIT (black line) and the FITR with R reference loci (colored lines) are shown for the demographic models 1 and 5. Each point corresponds to the power obtained by 100,000 simulations at the 5% significance level. The selection coefficients were s = 0.002 for model 1 and s = 0.0005 for model 5. The intervals between any two adjacent sampled points were the same, . The initial frequency for all R+1 loci, , was assumed to be 0.5. (A) The duration of sampling time was fixed at T = 1000. (B) The number of sampled points was fixed at L = 10. (Note: The FIT curve nearly overlapped with the FITR curve for L = 5 in Model 1.)
Applying the simulation method and FITR to practical situations
The FITR was developed and evaluated for type I error rate and power under ideal conditions of “selectively neutral” reference loci evolving independently of the focal locus and of each other, allele frequencies at reference loci ≠ 0 or 1, definable FITR statistics, and exactly known population allele frequencies. In practice, these ideal conditions may be violated. Before this section, the computer simulation method used in this study had not been validated. Here, we discuss the applicability of the simulation and describe cases that violate the aforementioned assumptions.
For the determination of allele frequencies in successive generations at R + 1 loci, the exact binomial sampling is computationally intensive and impractical for realistic population sizes (Figure 1). Therefore, we used a pseudosampling method to simulate the binomial sampling process (Wright−Fisher model). Even for a small, constant-size (n = 20) Wright−Fisher population, the fixation times for a mutant obtained by the pseudosampling were consistent with those obtained by binomial sampling (Kimura 1980). However, we considered only relatively short time scales, and the performance of the pseudo-sampling method was not obvious.
In Table 3, the rows denoted by r = “free” correspond with an assumption of free recombination (i.e., evolving independently) among R + 1 loci. Rejection rates simulated by the exact binomial sampling and by the pseudosampling are given. Demographic Models 1 and 5 with reduced population sizes were used (see Table 3, legend). We did not observe any differences in the results generated by the binomial sampling vs. the pseudosampling under neutral or selective cases. These findings support the applicability of pseudo-sampling to our problem of concern.
Results obtained by binomial sampling with various recombination fractions
| T . | L . | Δta . | rb . | Neutral (s0 = 0) . | Selective (s0 = 0.05) . | ||
|---|---|---|---|---|---|---|---|
| Binomialc . | Pseudod . | Binomialc . | Pseudod . | ||||
| [Model 1′]e | |||||||
| 10 | 2 | 5 | Free | 5.19 | 5.06 | 20.45 | 21.05 |
| 0.1 | 4.66 | − | 19.90 | − | |||
| 0.01 | 4.97 | − | 19.33 | − | |||
| 0 | 5.14 | − | 19.85 | − | |||
| 20 | 5 | 5 | Free | 5.00 | 4.94 | 36.06 | 36.48 |
| 0.1 | 4.97 | − | 36.05 | − | |||
| 0.01 | 4.95 | − | 37.08 | − | |||
| 0 | 4.84 | − | 35.76 | − | |||
| [Model 5′]f | |||||||
| 5 | 1 | 5 | Free | 5.07 | 5.01 | 8.57 | 8.34 |
| 0.1 | 4.93 | − | 8.80 | − | |||
| 0.01 | 5.08 | − | 8.09 | − | |||
| 0 | 5.41 | − | 8.13 | − | |||
| 10 | 5 | 2 | Free | 4.59 | 4.99 | 64.32 | 65.73 |
| 0.1 | 5.27 | − | 64.23 | − | |||
| 0.01 | 4.80 | − | 62.55 | − | |||
| 0 | 4.98 | − | 63.21 | − | |||
| T . | L . | Δta . | rb . | Neutral (s0 = 0) . | Selective (s0 = 0.05) . | ||
|---|---|---|---|---|---|---|---|
| Binomialc . | Pseudod . | Binomialc . | Pseudod . | ||||
| [Model 1′]e | |||||||
| 10 | 2 | 5 | Free | 5.19 | 5.06 | 20.45 | 21.05 |
| 0.1 | 4.66 | − | 19.90 | − | |||
| 0.01 | 4.97 | − | 19.33 | − | |||
| 0 | 5.14 | − | 19.85 | − | |||
| 20 | 5 | 5 | Free | 5.00 | 4.94 | 36.06 | 36.48 |
| 0.1 | 4.97 | − | 36.05 | − | |||
| 0.01 | 4.95 | − | 37.08 | − | |||
| 0 | 4.84 | − | 35.76 | − | |||
| [Model 5′]f | |||||||
| 5 | 1 | 5 | Free | 5.07 | 5.01 | 8.57 | 8.34 |
| 0.1 | 4.93 | − | 8.80 | − | |||
| 0.01 | 5.08 | − | 8.09 | − | |||
| 0 | 5.41 | − | 8.13 | − | |||
| 10 | 5 | 2 | Free | 4.59 | 4.99 | 64.32 | 65.73 |
| 0.1 | 5.27 | − | 64.23 | − | |||
| 0.01 | 4.80 | − | 62.55 | − | |||
| 0 | 4.98 | − | 63.21 | − | |||
Values indicate the rejection rates (%) obtained by 10,000 simulations for binomial sampling or by 100,000 simulations for pseudo-sampling under a nominal significance level of 5%.
The number of reference were R = 10 The initial frequencies for all R + 1 loci, xh,0, are assumed to be 0.5.
.
r, recombination fraction per generation between two adjacent loci of R + 1 loci. “Free” refers to free recombination.
Binomial, the binomial sampling.
Pseudo, the pseudo-sampling method used in this study.
Model 1′, the constant-size model with N = 100.
Model 5′, the severe bottleneck model with N(t) reduced to 1/200 of that in Model 5.
| T . | L . | Δta . | rb . | Neutral (s0 = 0) . | Selective (s0 = 0.05) . | ||
|---|---|---|---|---|---|---|---|
| Binomialc . | Pseudod . | Binomialc . | Pseudod . | ||||
| [Model 1′]e | |||||||
| 10 | 2 | 5 | Free | 5.19 | 5.06 | 20.45 | 21.05 |
| 0.1 | 4.66 | − | 19.90 | − | |||
| 0.01 | 4.97 | − | 19.33 | − | |||
| 0 | 5.14 | − | 19.85 | − | |||
| 20 | 5 | 5 | Free | 5.00 | 4.94 | 36.06 | 36.48 |
| 0.1 | 4.97 | − | 36.05 | − | |||
| 0.01 | 4.95 | − | 37.08 | − | |||
| 0 | 4.84 | − | 35.76 | − | |||
| [Model 5′]f | |||||||
| 5 | 1 | 5 | Free | 5.07 | 5.01 | 8.57 | 8.34 |
| 0.1 | 4.93 | − | 8.80 | − | |||
| 0.01 | 5.08 | − | 8.09 | − | |||
| 0 | 5.41 | − | 8.13 | − | |||
| 10 | 5 | 2 | Free | 4.59 | 4.99 | 64.32 | 65.73 |
| 0.1 | 5.27 | − | 64.23 | − | |||
| 0.01 | 4.80 | − | 62.55 | − | |||
| 0 | 4.98 | − | 63.21 | − | |||
| T . | L . | Δta . | rb . | Neutral (s0 = 0) . | Selective (s0 = 0.05) . | ||
|---|---|---|---|---|---|---|---|
| Binomialc . | Pseudod . | Binomialc . | Pseudod . | ||||
| [Model 1′]e | |||||||
| 10 | 2 | 5 | Free | 5.19 | 5.06 | 20.45 | 21.05 |
| 0.1 | 4.66 | − | 19.90 | − | |||
| 0.01 | 4.97 | − | 19.33 | − | |||
| 0 | 5.14 | − | 19.85 | − | |||
| 20 | 5 | 5 | Free | 5.00 | 4.94 | 36.06 | 36.48 |
| 0.1 | 4.97 | − | 36.05 | − | |||
| 0.01 | 4.95 | − | 37.08 | − | |||
| 0 | 4.84 | − | 35.76 | − | |||
| [Model 5′]f | |||||||
| 5 | 1 | 5 | Free | 5.07 | 5.01 | 8.57 | 8.34 |
| 0.1 | 4.93 | − | 8.80 | − | |||
| 0.01 | 5.08 | − | 8.09 | − | |||
| 0 | 5.41 | − | 8.13 | − | |||
| 10 | 5 | 2 | Free | 4.59 | 4.99 | 64.32 | 65.73 |
| 0.1 | 5.27 | − | 64.23 | − | |||
| 0.01 | 4.80 | − | 62.55 | − | |||
| 0 | 4.98 | − | 63.21 | − | |||
Values indicate the rejection rates (%) obtained by 10,000 simulations for binomial sampling or by 100,000 simulations for pseudo-sampling under a nominal significance level of 5%.
The number of reference were R = 10 The initial frequencies for all R + 1 loci, xh,0, are assumed to be 0.5.
.
r, recombination fraction per generation between two adjacent loci of R + 1 loci. “Free” refers to free recombination.
Binomial, the binomial sampling.
Pseudo, the pseudo-sampling method used in this study.
Model 1′, the constant-size model with N = 100.
Model 5′, the severe bottleneck model with N(t) reduced to 1/200 of that in Model 5.
Next, we considered the case in which the reference loci and focal loci were not independent. We limited our analysis to the case in which R + 1 loci were in linkage equilibrium (LE) at t=0. For closely linked loci, linkage disequilibrium (LD) is a distinct possibility. In addition, selection at the focal locus can drastically promote LD (e.g., Sabeti et al. 2002). However, for example, empirical studies of human genomes suggest that LD can be extended, at most, to several megabase pairs from the selective locus (e.g., Saunders et al. 2005). Because the genome is large compared with the megabase pairs scale, we can select R reference loci such that R + 1 loci are in LE. For this reason, our discussion is limited to the case in which R + 1 loci are in LE.
In Table 3, the rows indicated by r = 0.1, 0.01, and 0 describe results corresponding to a case in which the per-generation recombination fraction between any two adjacent loci are 0.1, 0.01, and 0, respectively. At t = 0, R + 1 loci are assumed to be in LE. That is, the alleles at R + 1 loci are randomly combined to form haplotypes. The simulations were conducted by the exact binomial sampling. For the neutral or selective cases, we observed no obvious differences between free recombination and limited recombination (r = 0.1, 0.01, and 0; Table 3). That is, the type I error rates and powers were maintained regardless of recombination fractions.
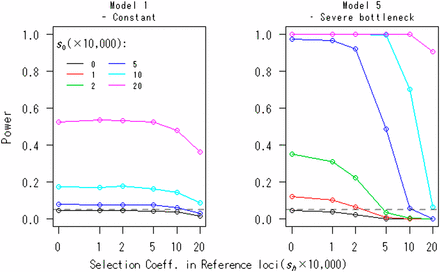
A case in which the reference loci are under selection is evaluated in Figure 4. The selection model is the same because the focal loci and R loci are under the same degree of selection. That is, for all loci, the fitnesses of genotypes AhAh, Ahah, and ahah are assumed to be 1, 1 + 0.5sh, and 1 + sh (s1 = s2 = ··· = sR), respectively. The effects of selection at the reference loci are conservative for type I error rates (see the case of s0 = 0 in Figure 4). The results of Model 1 suggest that if , there is little difference in rejection rates compared to the neutral case. Including Model 5, if the condition sh ≤ 1/2s0 is met, the power is not decreased. That is, the power is not highly sensitive to selection at the reference loci. Nevertheless, we recommend using synonymous sites or noncoding regions as references.
The effects of selection at reference loci on the power of the FITR. The powers of the FITR under various selection strengths, s0, at focal loci are shown as functions of the selection coefficient, , at reference loci for demographic models 1 and 5. Each point corresponds to the power obtained by 100,000 simulations at the 5% significance level. The number of reference loci, the duration of sampling time, and the number of sampled points were R = 10, T = 1000, and (L + 1) = 11, respectively. The intervals between any two adjacent sampled points were the same at . The initial frequency for all loci, , was assumed to be 0.5.
We next considered a situation in which allele frequencies at the reference loci were low at t = 0 and some allele frequencies could become 0 or 1 by t = T. When allele frequencies became 0 or 1, the statistic, tFITR, in (6) could not be defined. Therefore, it was practical to remove these loci from the calculation of tFITR. Table 4 indicates how rejection rates are changed by the data handling. Values in parentheses indicate the average number of reference loci used to calculate the FITR statistics. For L = 2 the type I error rate was inflated by a few percent (e.g., 6.69% at most, Model 1) possibly because changes in allele frequencies at reference loci are biased toward smaller values when loci are removed for which the frequencies of alleles become 0 or 1. These apparently reduced changes in allele frequencies could bring about overestimates of change at the selective locus. For L = 10 the inflation of the type I error rate becomes small. In general, to prevent inflation of the type I error rate, loci having moderate frequencies of alleles (e.g., ≥10%) should be used in this test.
Effects of allele frequencies at the reference loci
| T . | L . | Δta . | xh,0b (h ≠ 0) . | Model 1 . | Model 5 . | ||
|---|---|---|---|---|---|---|---|
| Neutral (s0 = 0) . | Selective (s0 = 0.002) . | Neutral (s0 = 0) . | Selective (s0 = 0.0005) . | ||||
| 1000 | 2 | 500 | 0.5 | 4.86 (10.00) | 50.03 (10.00) | 5.05 (10.00) | 82.93 (10.00) |
| 0.1 | 5.55 (9.84) | 52.00 (9.84) | 5.00 (10.00) | 82.98 (10.00) | |||
| 0.05 | 6.69 (8.70) | 53.11 (8.70) | 5.28 (10.00) | 82.85 (10.00) | |||
| 0.01 | 5.55 (3.37) | 28.03 (3.37) | 6.77 (7.84) | 80.47 (7.84) | |||
| 1000 | 10 | 100 | 0.5 | 4.91 (10.00) | 53.49 (10.00) | 4.93 (10.00) | 97.44 (10.00) |
| 0.1 | 5.05 (9.84) | 54.03 (9.85) | 4.99 (10.00) | 97.52 (10.00) | |||
| 0.05 | 5.18 (8.70) | 53.95 (8.70) | 4.99 (10.00) | 97.34 (10.00) | |||
| 0.01 | 5.26 (3.38) | 34.35 (3.38) | 5.46 (7.84) | 96.87 (7.83) | |||
| T . | L . | Δta . | xh,0b (h ≠ 0) . | Model 1 . | Model 5 . | ||
|---|---|---|---|---|---|---|---|
| Neutral (s0 = 0) . | Selective (s0 = 0.002) . | Neutral (s0 = 0) . | Selective (s0 = 0.0005) . | ||||
| 1000 | 2 | 500 | 0.5 | 4.86 (10.00) | 50.03 (10.00) | 5.05 (10.00) | 82.93 (10.00) |
| 0.1 | 5.55 (9.84) | 52.00 (9.84) | 5.00 (10.00) | 82.98 (10.00) | |||
| 0.05 | 6.69 (8.70) | 53.11 (8.70) | 5.28 (10.00) | 82.85 (10.00) | |||
| 0.01 | 5.55 (3.37) | 28.03 (3.37) | 6.77 (7.84) | 80.47 (7.84) | |||
| 1000 | 10 | 100 | 0.5 | 4.91 (10.00) | 53.49 (10.00) | 4.93 (10.00) | 97.44 (10.00) |
| 0.1 | 5.05 (9.84) | 54.03 (9.85) | 4.99 (10.00) | 97.52 (10.00) | |||
| 0.05 | 5.18 (8.70) | 53.95 (8.70) | 4.99 (10.00) | 97.34 (10.00) | |||
| 0.01 | 5.26 (3.38) | 34.35 (3.38) | 5.46 (7.84) | 96.87 (7.83) | |||
Values indicate rejection rates (%) obtained by 100,000 simulations under a nominal significance level of 5%. Values in parentheses correspond to the mean number of reference loci used to calculate the FITR statistics. The number of reference loci at t0 were R = 10. The initial frequency of the focal locus, x0,0, was assumed to be 0.5.
.
xh,0, the allele frequencies of the reference loci at t0.
| T . | L . | Δta . | xh,0b (h ≠ 0) . | Model 1 . | Model 5 . | ||
|---|---|---|---|---|---|---|---|
| Neutral (s0 = 0) . | Selective (s0 = 0.002) . | Neutral (s0 = 0) . | Selective (s0 = 0.0005) . | ||||
| 1000 | 2 | 500 | 0.5 | 4.86 (10.00) | 50.03 (10.00) | 5.05 (10.00) | 82.93 (10.00) |
| 0.1 | 5.55 (9.84) | 52.00 (9.84) | 5.00 (10.00) | 82.98 (10.00) | |||
| 0.05 | 6.69 (8.70) | 53.11 (8.70) | 5.28 (10.00) | 82.85 (10.00) | |||
| 0.01 | 5.55 (3.37) | 28.03 (3.37) | 6.77 (7.84) | 80.47 (7.84) | |||
| 1000 | 10 | 100 | 0.5 | 4.91 (10.00) | 53.49 (10.00) | 4.93 (10.00) | 97.44 (10.00) |
| 0.1 | 5.05 (9.84) | 54.03 (9.85) | 4.99 (10.00) | 97.52 (10.00) | |||
| 0.05 | 5.18 (8.70) | 53.95 (8.70) | 4.99 (10.00) | 97.34 (10.00) | |||
| 0.01 | 5.26 (3.38) | 34.35 (3.38) | 5.46 (7.84) | 96.87 (7.83) | |||
| T . | L . | Δta . | xh,0b (h ≠ 0) . | Model 1 . | Model 5 . | ||
|---|---|---|---|---|---|---|---|
| Neutral (s0 = 0) . | Selective (s0 = 0.002) . | Neutral (s0 = 0) . | Selective (s0 = 0.0005) . | ||||
| 1000 | 2 | 500 | 0.5 | 4.86 (10.00) | 50.03 (10.00) | 5.05 (10.00) | 82.93 (10.00) |
| 0.1 | 5.55 (9.84) | 52.00 (9.84) | 5.00 (10.00) | 82.98 (10.00) | |||
| 0.05 | 6.69 (8.70) | 53.11 (8.70) | 5.28 (10.00) | 82.85 (10.00) | |||
| 0.01 | 5.55 (3.37) | 28.03 (3.37) | 6.77 (7.84) | 80.47 (7.84) | |||
| 1000 | 10 | 100 | 0.5 | 4.91 (10.00) | 53.49 (10.00) | 4.93 (10.00) | 97.44 (10.00) |
| 0.1 | 5.05 (9.84) | 54.03 (9.85) | 4.99 (10.00) | 97.52 (10.00) | |||
| 0.05 | 5.18 (8.70) | 53.95 (8.70) | 4.99 (10.00) | 97.34 (10.00) | |||
| 0.01 | 5.26 (3.38) | 34.35 (3.38) | 5.46 (7.84) | 96.87 (7.83) | |||
Values indicate rejection rates (%) obtained by 100,000 simulations under a nominal significance level of 5%. Values in parentheses correspond to the mean number of reference loci used to calculate the FITR statistics. The number of reference loci at t0 were R = 10. The initial frequency of the focal locus, x0,0, was assumed to be 0.5.
.
xh,0, the allele frequencies of the reference loci at t0.
The effects of sampling error on the type I error rate and power of the FITR are shown in Figure 5. In general, the effects of sampling error on the type I error rate were conservative. As expected, the power decreased as the number of sampled individuals increased. The degree of power reduction differed for different demographic models or values of L. This finding reflects that the power is influenced by the relative magnitudes of changes in allele frequencies at R + 1 loci and sampling errors. As L increased, the relative changes in allele frequencies to the sampling errors decreased. Thus, power was more reduced for larger L. Regarding the demographic models, the population size of Model 5 was larger than that of Model 1. Therefore, the relative changes in allele frequencies to the sampling errors were larger in Model 5, and the degree of power is large in Model 5.
In this study, we proposed a neutrality test, the FITR, to accommodate fluctuations in population size using reference loci. Our test is an extension of Feder et al.’s (2013) FIT. By computer simulation, the actual type I error rate of the FITR was nearly equal to the nominal significant level regardless of fluctuations in population size when sampling noise could be ignored. The FITR detected selection with remarkable power under conditions of rapid growth (model 4) and severe bottleneck (model 5). Even under a model of constant population size, the FITR using 10 or more reference loci had more power than the FIT.
We also discussed the performance of the FITR in practical situations. The effects of selection at the reference loci were small unless selection was strong. Our findings indicated that when R + 1 were in LE, those loci should be considered independent of each other. In addition, loci with moderate frequencies of alleles should be used as references. Our findings may facilitate the development of more sophisticated methods using independent reference loci, including a method that can quantify (estimate) the strength of selection. These methods will enable appropriate inferences about natural selection in real and dynamic populations. Figure 5.
The effects of sampling error on the power of the FITR. The powers of the FITR under various sampling regimes are shown as functions of the selection coefficients for demographic models 3 and 5. All, or 5000, 1000, 500, or 100 individuals in a population were assumed to be sampled. Sampling was assumed to be conducted by binomial sampling at each (R + 1) locus and at each (L + 1) time point. Each point corresponds to the power obtained by 100,000 simulations at the 5% significance level. The number of reference loci, the duration of sampling time, and the number of sampled points were R = 10, T = 1000, and (L + 1) = 3 (upper graphs) or 11 (lower graphs), respectively. The intervals between any two adjacent sampled points were the same at Δt = ti–ti-1 = 500 (top graphs) or 100 (bottom graphs) (i = 1,2,…,L). The initial frequency for all loci, , were assumed to be 0.5.
Appendix
Considering for all , the joint probability density of , , under .
- i)
is the exact LRS using data
We will show that given by (3) or (4) is the exact statistic using data to test (for all h) against and in the likelihood ratio test framework.
In our model, the likelihood ratio test is a test for which we reject ifOtherwise, we accept H0. Here, is the maximum likelihood estimator (MLE) of Ni under H0, and and are the MLEs of and under H1.(A2)Under H0, the probability density of is given byfrom (A1). Solvingwe getThenUnder H1, the probability density of is given byfrom (A1). Solvingwe getThenThus, is equivalent toWith some algebra, we let a new constantFinally, we getwhere . Therefore, tFITR(i) as given by (3) or (4) is the exact LRS using data . - ii)
Ad hoc interpretation for tFITR as a test statistic using the data Δx
As R grows, the t distribution for tFITR(i) approaches the normal distribution with mean and variance 1,Unfortunately, varies with Ni, , and . When ; 0.50, 0.490, 0.458, 0.400, 0.300 and 0.218, respectively. Nevertheless, the values of are roughly the same if are far from 0 or 1. In addition, the values of and vary with i. However, we try to consider as a constant μ, such thatConsider a test H0:μ = 0 against H1:μ ≠ 0 using L i.i.d samples from the distribution. The LRS is given by the sum of , . That is, when R is large and the variation of the value for is not large, tFITR given by (5) or (6) is expected to be close to the LRS.
Acknowledgments
I thank K. Ikeo and S. Mano for useful suggestions on the study. I also thank the associate editor and the two anonymous reviewers for their helpful comments on an earlier version of this manuscript, which improved this work substantially. This work was supported by health labor sciences research grant from The Ministry of Health Labor and Welfare (H23-jituyouka(nanbyou)-006).
Footnotes
Communicating editor: P. Pfaffelhuber